딥러닝의 기초: 데이터를 이해하자

딥러닝을 제대로 이해하기 위해서는 데이터를 어떻게 다루고 분석할지 아는 것이 중요합니다.

데이터는 변수(Variables)와 상수(Constants)로 구성되며, 이를 통해 모델을 학습하고 예측을 할 수 있습니다.

---

1. 변수(Variables)와 상수(Constants)

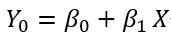
• 상수는 변하지 않는 값을 의미합니다. 딥러닝 모델에서 흔히 사용하는 상수로는 회귀 모델의 절편(β₀)과 기울기(β₁)를 예로 들 수 있습니다.
• 변수는 변화할 수 있는 값을 의미하며, 데이터 분석에서 매우 중요합니다.
  • X: 독립변수(Independent Variables)라고 하며, 원인이나 설명 요인을 나타냅니다.
  • Y: 종속변수(Dependent Variables)라고 하며, 결과나 반응을 나타냅니다. Y는 X의 변화에 따라 값이 달라집니다.

한 그룹의 모든 사람에게 동일한 특성을 갖는 것이 상수이고, 다른 값을 가질 수 있는 것이 변수입니다.

---

2. 모집단(Population)과 샘플집단(Samples)

딥러닝에서 데이터의 정확성을 높이기 위해 모집단과 샘플집단의 개념을 이해하는 것이 중요합니다.

• 모집단 (Population): 우리가 관심을 두는 전체 데이터 집합입니다. 예를 들어, “우리나라 국민의 A 후보 지지율”을 조사할 때, 모집단은 “우리나라 국민 전체”입니다.
• 샘플집단 (Samples): 모집단에서 현실적인 한계로 인해 선택된 일부입니다. 여론조사를 예로 들면, 특정 기간 동안 조사에 참여한 사람들이 샘플집단이 됩니다.

주요 용어

• Parameter: 모집단을 대상으로 계산된 값. 정확한 결과로 간주됩니다.
• Statistics: 샘플집단을 대상으로 계산된 값. 모집단의 특성을 추정하기 위한 목적으로 사용됩니다.

---

3. 데이터 측정 수준 (Measurement)

변수의 측정은 정확도에 따라 Hierarchy (계급)으로 나눌 수 있습니다. 측정 수준에 따라 변수는 다음 네 가지로 분류됩니다:

1. 명목변수 (Nominal Variable)
   • 정의: 이름이나 범주로 분류되는 변수로, 순서나 크기를 비교할 수 없습니다.
   • 특징: 범주 간의 순서가 없습니다.
   • 예시: 성별(남성, 여성), 혈액형(A형, B형), 국가 이름(대한민국, 미국)
2. 순위변수 (Ordinal Variable)
   • 정의: 순서가 있는 변수로, 값의 서열은 존재하지만 각 순서 간 간격이 일정하지 않습니다.
   • 특징: 순서는 있지만 간격의 차이는 의미가 없습니다.
   • 예시: 교육 수준(초등학교, 중학교, 고등학교), 군대 계급(이병, 병장)
3. 간격변수 (Interval Variable)
   • 정의: 값 간의 간격이 일정하지만 절대적인 0이 존재하지 않는 변수입니다.
   • 특징: 덧셈과 뺄셈은 의미가 있지만, 비율 계산은 의미가 없습니다.
   • 예시: 섭씨 온도(0°C는 온도가 없는 것이 아님), 연도
4. 비율변수 (Ratio Variable)
   • 정의: 값 간의 간격이 일정하고 절대적인 0이 존재하는 변수입니다.
   • 특징: 덧셈, 뺄셈, 곱셈, 나눗셈 모두 가능하며 비율 계산이 의미가 있습니다.
   • 예시: 몸무게(0kg은 무게 없음), 소득(0원은 소득 없음)
5.  질적변수와 양적변수 

1) 질적 변수 (Qualitative Variable)

• 정의: 질적 변수는 데이터가 숫자보다는 명칭이나 특성으로 표현되는 변수입니다. 이러한 변수는 속성, 범주, 특성 등을 나타내며, 수치적 연산이 불가능합니다.
• 종류:
  • 명목변수 (Nominal Variable): 순서가 없는 범주형 변수. 예) 성별, 혈액형
  • 순위변수 (Ordinal Variable): 순서가 있는 범주형 변수. 예) 만족도, 교육 수준
• 예시:
  • 머리카락 색: 검정, 갈색, 금발
  • 직업: 의사, 교사, 엔지니어
  • 음식 선호도: 1위, 2위, 3위

---

2) 양적 변수 (Quantitative Variable)

 

 

• 간격변수와 비율변수는 둘 다 수치형 데이터이지만, 0점의 의미에 차이가 있습니다.
  • 간격변수: 0이 ‘없음’을 나타내지 않으며, 비율 계산이 불가능합니다. 예) 섭씨 온도, 연도
  • 비율변수: 0이 ‘완전한 없음’을 나타내며, 비율 계산이 가능합니다. 예) 몸무게, 키, 소득, 나이
• 이산형 변수와 연속형 변수는 데이터 값의 연속성에 따라 나뉩니다.
  • 이산형 변수: 셀 수 있는 정수 값만 가질 수 있습니다. 한 가족의 구성원 수(2명, 3명, 4명)처럼 특정 정수 값을 가짐.
  • 연속형 변수: 측정 가능한 연속적인 값으로, 소수점까지 포함할 수 있습니다. 강의 길이(4.75km)처럼 특정 범위 내의 모든 값이 가능함.

 

나이를 예를 들면, 양적변수이며, 비율변수이며, 이산형변수 입니다. (24.3살은 없으니까요)

    또, 나이는 비율 계산이 가능: 예를 들어, 40세는 20세의 두 배라고 할 수 있습니다. 즉, 두 나이 사이의 비율이 의미가 있습니다.

연도는 양적변수이며, 간격변수이며, 이산형 변수 입니다. 

 

 

---

4. 변수의 중심 경향(Central tendency)과 분포(Distribution)

*변수의 중심 경향 (Central Tendency)

중심 경향은 데이터의 중심을 나타내는 지표로, 데이터 분포를 요약하는 데 사용됩니다. 주요 지표는 평균(Mean), 중앙값(Median), 최빈값(Mode)입니다.

• Mean (평균)
  • 모든 데이터의 합을 데이터 개수로 나눈 값입니다. 극단값에 민감하게 영향을 받습니다.
  • 기호:
    • x̄ (엑스 바): 표본 평균
    • μ (뮤): 모집단 평균
• Median (중앙값)
  • 데이터를 크기순으로 정렬했을 때 중간에 위치한 값입니다. 이상치의 영향을 받지 않습니다.
• Mode (최빈값)
  • 가장 자주 나타나는 값입니다. 최빈값이 여러 개일 수 있습니다.
• 예시
  • 한 학급의 수학 점수가 70, 80, 90, 100, 60이라고 가정합니다.
  • 평균 = (70+80+90+100+60) /5 = 80
  • 중앙값 : 오름차순으로 정렬하면 {60, 70, 80, 90, 100},  중간에 있는 값인 80이 중앙값
    • 짝수 개의 데이터일 경우, 중간 두 값의 평균을 계산
  • 또 다른 점수 집합 {70, 80, 70, 90, 100}이 있다고 가정합니다.
  • 70이 두 번 나오므로 최빈값은 70입니다.
    • 최빈값이 여러 개일 수도 있고, 없을 수도 있습니다.
• Skewness(왜도)
  • 왜도는 데이터 분포의 비대칭성을 나타내는 지표입니다.
    • 양의 왜도 (Right-Skewed, Positive skew): 꼬리가 오른쪽으로 길고 평균이 중앙값보다 큽니다. (예: 소득 분포)
    • 음의 왜도 (Left-Skewed, Negative skew): 꼬리가 왼쪽으로 길고 평균이 중앙값보다 작습니다.
    • 왜도 값이 0에 가까움: 대칭에 가까운 분포입니다.

    

 

---

*분포 (Distribution)

• 모분산(population variance): 전체 모집단의 데이터 분포를 측정하는 척도로, 각 데이터가 평균으로부터 얼마나 떨어져 있는지를 나타냅니다. 계산식은

• , 여기서 N은 모집단 크기, Xi​는 데이터 값, μ는 모집단 평균입니다.
• 표본분산(sample variance): 모집단이 아닌 표본을 사용해 분포를 측정할 때 사용하는 척도입니다. 계산식은

• 여기서 N은 표본 크기, Xi​는 표본 데이터 값, Xˉ는 표본 평균입니다.
• 모표준편차(population standard deviation): 모분산의 제곱근으로, 모집단 데이터의 분산 정도를 나타냅니다.
• 표본표준편차(sample standard deviation): 표본분산의 제곱근으로, 표본 데이터의 분산 정도를 나타냅니다.